You’re asking for more about the calculations — twist my arm.

I’ll start by saying that I got the equations and data from work. Remember I worked on photochemical dispersion models, models that by definition must figure out how much sunlight there is (and, from that, the rate at which the photochemical reactions will proceed) as a function of date, time, and latitude/longitude. First, the models use the time and location data to calculate solar elevation, i.e. how high in the sky is the sun. The second step is to use the calculated solar elevation to determine the amount of sunlight. The version of the software jumps directly from this calculated solar elevation to reaction rates, but fortunately I found a file I’d saved from an earlier version that provided sunlight data (by wavelength incremented by 10 nanometers) as a function of solar elevation (as an intermediate step toward calculation photochemical rate constants).

Determining solar elevation is a spherical geometry problem. I find it curious that, despite all the math I studied in college, I was never taught spherical geometry. Details of the problem here are in an “appendix” below. Suffice it for the moment to say that I got the equation from the model.

I also used the data from the model on sunlight amounts versus solar elevation, again not working from first principles. UV light is sometimes subdivided into UV-A (wavelength 315 - 400 nm), UV-B (280 - 315 nm), and UV-C (100 - 280 nm). Sunburn risk best correlates with UV-B light, because the ozone layer blocks almost all the UV-C and UV-A is less energetic. I used data for 3 wavelengths: 290, 300, and 310 nanometers (sunlight for 280 nm is negligible).

With data on UV-B for 10 solar elevations, I then had to interpolate UV-B amounts for other solar elevations. It appears that UV-B correlates well with {sin(solar elevation) / optical air mass}. (Optical air mass expresses the greater length of atmosphere that a “lower in the sky sun” passes through.) However, since I just wanted a good approximation to intermediate values, without concern as to proper representation of underlying physics, I used a 6th order polynomial to make this approximation. In case there are computer geeks reading this, I used R software to determine the polynomial, and I provide the script below.

That’s the hard part. The maximum value in Evanston, at solar noon on June 21, is about 0.465. (Units are something like the number of thousand trillion photons per square centimeter per second.) I treat that as an amount associated with sunburning in 10 minutes, with proportionately less sunlight yielding proportionately longer sunburn times.

Addendum on spherical geometry: I’m not sure how well I can articulate the spherical geometry question involved in calculating solar elevation as a function of time and location. Remember that the earth is tilted about 23 degrees down relative to the plane of the earth’s revolution around the sun (this is called declination). If you think about looking at this tilted earth from the front (summer), side (spring and fall), or back (winter), you can understand how the day of year influences solar elevation. (For example, at solar noon, i.e. when the sun is highest in the sky, the solar elevation will be 23 degrees less than your latitude at the summer solstice, your latitude at the vernal and autumnal equinoxes, and 23 degrees more than your latitude at the winter solstice. It varies kinda sinusoidally in between.)

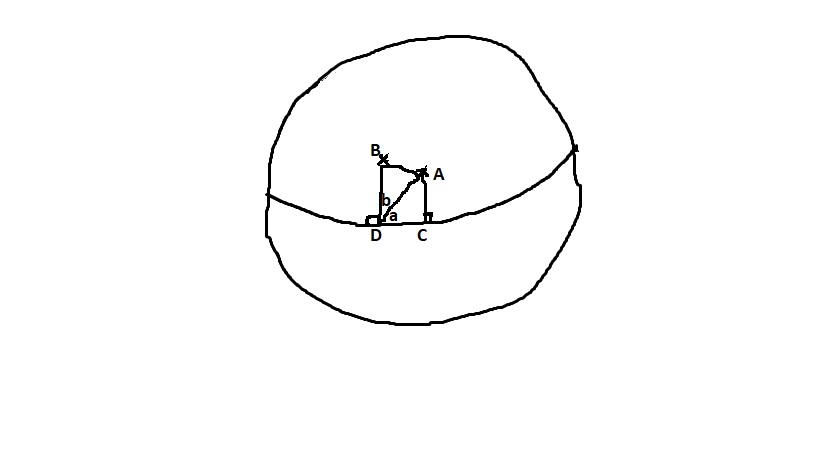
I’ve attached an illustration that helps explain how I think one solves this problem. Point A is the point on the earth directly under the sun on that day at the time of interest. Point B is your location at that time. The challenge is to determine the length of AB, measured in degrees, which is the zenith angle, i.e. the number of degrees off overhead (which equals 90 degrees - solar elevation). Point C is on the equator at the longitude of Point A, and Point D is on the equator at your longitude. Length AC is the effective declination (a function of the day of year), the angle AC/CD is a right angle, and length CD (called HRANGL in the spreadsheet) equals the fraction of a day before or after solar noon times 360 degrees. For those that know the formulae for spherical triangles, this is enough to figure out the angle CD/DA and the length DA. I believe that the angle CD/DA and DA/DB have to add up to 90 degrees. Even if I’m wrong, one can determine the angle DA/DB, we have determined the length DA, and we know the length DB (your latitude). Thus, a spherical geometer is armed with all the knowledge he or she needs to figure out the dimensions of the spherical triangle ADB, in particular to determine the length of AB. Again, fortunately, I could take all the necessary equations from the photochemical model and I didn’t have to figure any of this out for myself.

Addendum on determining the best fit polynomial: When you plot for example UV-B light against solar elevation in Excel, you can have it show a best fit polynomial and the equation that goes with it. However, when I did that, I got not enough significant figures and not a very good approximation. Therefore, I used data analysis software called R. The script is a short one:

solelev <- c(90,80,70,60,50,40,30,20,10,4)

UV <- c(0.464871247,0.455219694,0.420492242,0.363619288,

0.287628086,0.198730583,0.109071858,0.038259132,0.008963353,0.000910551)

irrfunc4 <- lm(UV ~ solelev + I(solelev^2) + I(solelev^3) + I(solelev^4) + I(solelev^5)+I(solelev^6))

coef(irrfunc4)

(Also, to confirm data entry, print(solelev) and print(UV))

OK, maybe this is a little more than you bargained for, but I hope this foray into astronomics has been fun.